思考力を鍛える単元としておすすめ。
こんにちは、ヤマモトです。
僕は趣味で数学を学び直しているフリーターです。
今回は、整数の性質を学び直したので感想を話していきます。
ちなみに僕は基礎問題精講で勉強しています。
調べてみたら新課程では整数の性質は「数学と人間の活動」という単元に吸収されてしまっているそうです。
僕が使っている基礎問は4訂版と古いもののため、その点はご了承ください。
あくまで僕は趣味として数学を学び直しているだけなので、そのまま進めたいと思います。
本記事の内容
- シンプルだが意外に手こずった
- まずは整数についての意味を知ることが大事
- 思考力を鍛える訓練としておすすめの単元
シンプルだが意外に手こずった
難しい関数や複雑な計算はあまりなく、中学レベルの知識だけでもある程度はできそうな感じはしました。
整数という、
- 正の数(1,2,3、、、など)
- 0
- 負の数(-1,-2,-3、、、など)
この3つのシンプルな組み合わせを深掘るような単元ですね。
分数やルートなどもほとんど出てこない感じなので、わかりやすいっちゃわかりやすいです。
ですが、思考力を伴う問題が多いため意外に手こずりました。
特に倍数に関する問題は、最初よく意味がわからんくて?となりました。
それもYouTubeとかで検索したら色々と答えが出てきて、なんとか理解できましたね。
例えば、
2a=3b
を証明しろみたいな問題があったとしましょう。
*ちなみにこれと似たような問題が、基礎問題精講の不定方程式という問題でありました。
左辺が2の倍数だから3bも2の倍数であり、3は2を因数に持たないからbが2の因数を持つ。
よって、bは2の倍数。
同様に右辺は3の倍数だから2aも3の倍数であり、2は3を因数に持たないからaが3の因数を持つ。
よって、aは3の倍数。
ゆえに2a=3bはお互い6の倍数となり、等式は成り立つ。
(証明終了)
*僕の証明が正しいかどうかは添削してもらったわけではないので、注意してください。
詳しいことは書籍や参考書などをご覧ください。
これを読んでも?と思うかもしれませんが、僕はなんとか理解することができました。
要は両辺が6の倍数であると証明すればいいということです。
例えば、aに3をbに2を入れたら、
2a=3b
2*3=3*2
6=6
となりますからね。
これだけだと本当か?と思われるかもしれないので他の2の倍数、3の倍数を入れてみましょう。
ちなみに2の倍数は、2,4,6,8,10、、、と+2ずつしていく数です。
3の倍数は、3,6,9,12,15、、、と+3ずつしていく数です。
それでは4と6を入れてみましょう。
2*6=3*4
12=12
次に、8と12を入れてみます。
2*12=3*8
24=24
こんな感じで成り立つことがわかります。
一見すると当たり前じゃんと思われることも、証明しろと言われると戸惑うものです。
こうやって当たり前のものでも突き詰めて考えていく力は実生活においても役立つと思います。
少なくとも脳トレとしてはかなり高い効果が期待できるのではないでしょうか。
他にも2進数の計算とかガウス記号とか、他の単元であんま出てこないことも学びました。
2進数の計算は慣れていないためか、ちょっと苦手です。
これは何度も計算して覚えていくしかないと思います。
ガウス記号は意味がわかればそんなに難しくなかったです。
整数問題はけっこう難しい
基礎問題精講に整数問題というのが3問くらいありましたが、これは結構難しいです。
僕も初見では意味不明でしたから。
何回か解いてみて、なんとか少しだけ理解できました。
基礎問にある問題はまだ易しい方ですが、難関大学とかになると超難問とかも出てくるみたいです。
公式に当てはめて解くのではなく、自分で試行錯誤しないといけないのが難しいです。
まあこういう問題の方が頭を使うので解けると楽しいのですがね。
僕は複雑な計算をゴリゴリ解くのは苦手なので、思考系の問題の方が好きです。
まずは整数についての意味を知ることが大事
整数の意味を正しく理解していないと、解答を読んでも意味わからんくなると思います。
整数とは先ほど言ったように、
- 正の数(自然数とも言う)
- 0
- 負の数
この3つですね。
この中には分数もルートも含まれません。
これがわかっていないと解けない問題もありましたね。
例えば最大値、最小値を求める問題などです。
これを求めるには2次関数で習う、平方完成をしないといけません。
例えば、
y=(x-5)^2+9/4
この式の最小値となる整数を求めよという問題があったとします。
こういう問題ならXに5を入れれば最小値9/4が出ます。
よって最小値は9/4。
めでたし、めでたし。。。
としたいところですが、残念ながら不正解です。
それは問題文に整数を求めよと書いてあるからですね。
つまり分数だとNGなわけです。
9/4を小数点で表すと2.25です。
不等式で表すと、
2<2.25<3
で挟まれる範囲ですね。
つまり2か3が答えになります。
どっちの数字が小さくなると言えば、2ですね。
2の方が0.25距離が離れていますが、3の場合0.75距離が離れてるからです。
頂点からの距離が短い方が低い数字になるため、2が正解なわけです。
図にするとこんなイメージ。
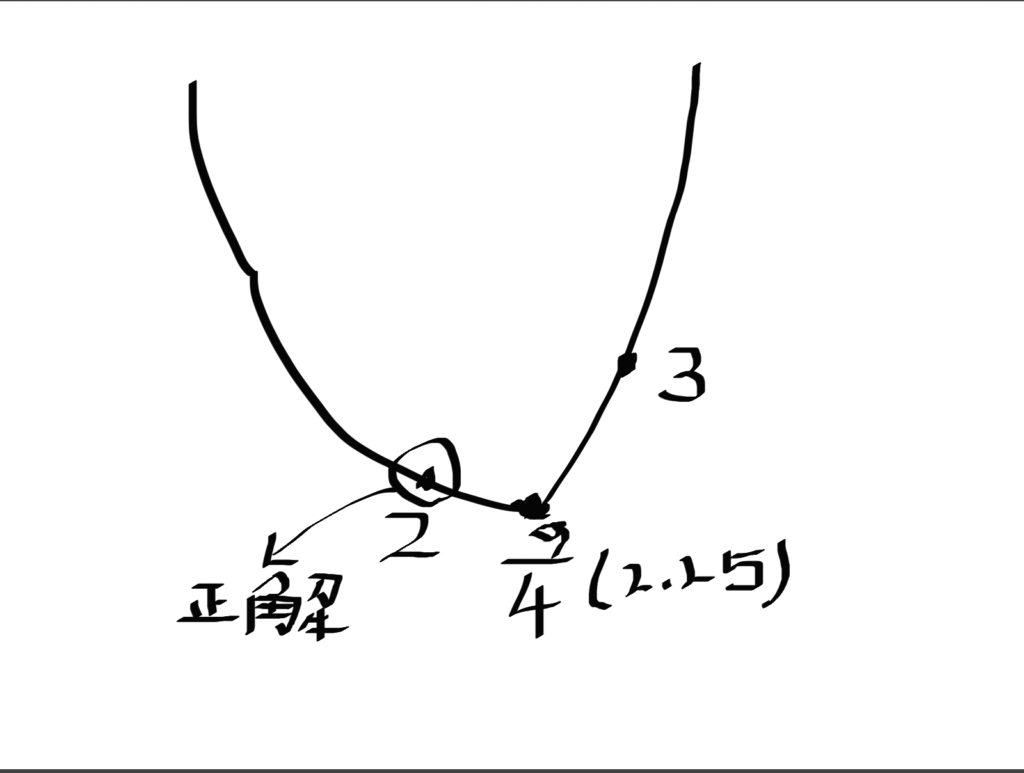
図が汚くて申し訳ないですが、2の方が下に来ていますよね?
つまり最小値は2というわけです。
整数の意味がわかっていないと解答を見ても、???????という感じになると思います。
ですから、整数という意味をしっかり理解しておくのがまず大事なわけですよ。
思考力を鍛える訓練としておすすめの単元
整数の性質は、複雑な計算や覚えないといけない公式も少ないです。
そのため思考力を鍛える訓練としてはおすすめの単元ですね。
図形の性質も思考力が鍛えられますが、図形の知識がないと全く問題解けませんから。
それに比べて整数の性質は知識はそんなに要りません。
よって、わりととっつきやすいと思います。
まあ、難しい問題はとことん難しい単元ではありますが。。
少なくとも基礎レベルではそんなに苦戦することはないかと思います。
以上、整数の性質を学び直した感想でした。